Numerical Analysis of Prevailing Mechanical Stresses Exerted on Particles during Mechanofusion Mixing Using Discrete Element Method

What is Mechanofusion?

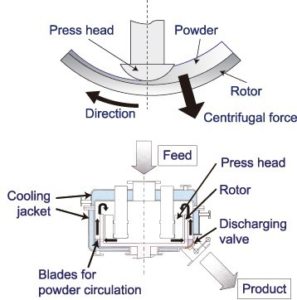
Mechanofusion is a dry powder coating process that utilises mechanical energy to modify tribological and surface functional characteristics of particles or even induce mechano-chemical reactions between different particles, and hence producing particles with new characteristics. The equipment comprises a cylindrical vessel that is rotated at high speeds on its axis, thereby generating a centrifugal field. Particles placed inside the vessel move to the outer wall and form a dense bed under large compressive stresses. A stationary semi-cylindrical surface, connected to an arm (press head as shown in the Figure below) compresses and ‘shaves’ the particle bed by forcing it to pass through a small gap between the press head and the rotating vessel wall. The gap size is very narrow, providing a great shear straining, due to the velocity gradient of the particles along the radial direction, and ‘smearing’ the surfaces of the particles with any additives that are used. As they pass through the gap, shearing occurs. The high compressive and shear forces and straining experienced by the particles promote dry coating through a “spread and smear” motion.

What is DEM?

Discrete Element Method (DEM) is a numerical technique that computes the forces and displacements of discrete particles using Newton’s second law of motion. The interaction of the particles amongst themselves and against the geometry of interest is captured by the technique, making it an effective solution for addressing granular processing issues that are otherwise difficult to investigate experimentally.

What Is Happening Inside a Mechanofusion Device during Mixing?

Mechanofusion is known to be a very efficient dry powder coating technique, but due to the presence of extreme mechanical stresses and strains, optimisation of the performance requires a deep understanding of the prevailing microscopic processes that are happening inside the device during the mixing process. Experimental observation of the process is very challenging, even with the present day modern X-ray tomography instrument due to great speeds of operation. Advances in computational capability over the past decade offer simulation alternatives to elucidate some of the underlying mechanisms, albeit for some simple cases. One of them is the numerical tool of Discrete Element Method, enabling simulation of complex particulate processes, such as the one under study here: modelling and analysis of the Mechanofusion process using the software package of Rocky (ESSS, Florianopolis, Brazil). By doing so, we provide a virtual “see through” the instrument and study the dynamics of particles during the mixing process of Mechanofusion.

Modelling Particle Shape

Particle shape has a strong influence on the bulk friction of powders and grains. In this study sphere and shapes approximating crystals of α-lactose monohydrate and paracetamol (in view of their industrial importance), as shown in the video below, are considered and their effect on the bulk frictional behaviour of particles is assessed.

Dynamics of Particle Interaction

The video below shows the particle motion of spheres and crystals of α-lactose monohydrate and paracetamol during mixing in Mechanofusion. The colour of the particles represents their velocity. As described earlier, due to the centrifugal force exerted on the particles while the vessel is rotating at a very high speed, the particles are pressed against the vessel wall, along which a bed of particles is formed. As the bed of particles passes through the tiny gap between the fixed push arm and the vessel wall, a velocity gradient is generated across the particle bed due to the constriction. This generates shearing and promotes the mixing of the particles. The excess particles which cannot not enter the gap are shaved off by the push arm and redeposit on the surface of the bed. As for those that manage to pass through the gap, a scraper is placed right after the push arm to plough off the particles that are sticking to the wall, facilitating a more homogeneous mixing of the particles.

Operating under the same conditions, we clearly see that the dynamics of particle interaction of different shapes vary significantly. The overall particle assembly appears to be more dilated in the case of α-lactose monohydrate. This is a direct consequence of particle packing, due to their non-rounded shape giving rise to more empty voids between the particles. This gets even more prominent when the particles are of large aspect ratio, e.g. needle-shaped particles. Interestingly, the angle of the rebounding stream of particles is the steepest for paracetamol, followed by lactose and spheres. Given they are all run under the same operating conditions, the difference in the rebounding angle is attributed to the differences in particle shape.

Hydrostatic and Shear Stress Distributions

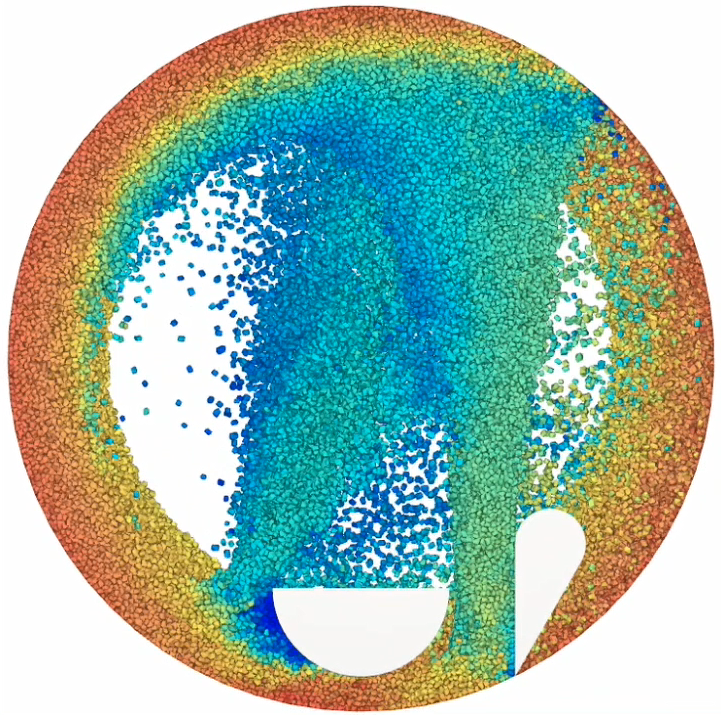
Using Eulerian statistics, the average spatial distribution of the prevailing stresses during Mechanofusion mixing is evaluated by Rocky DEM. Both hydrostatic and shear stresses are of interest in this work as they work on the particle surfaces and its bulk, causing a particle to change its volume and shape by attrition and fragmentation.

Before watching the videos, let’s take a moment to guess where the particles would experience the greatest stresses! Attention is most likely drawn to the narrow gap between the push arm and the vessel wall. Prediction by Rocky software is shown by playing the videos now.

The above videos correspond to the average spatial distribution of hydrostatic and shear stresses, respectively. The colour of the contour plot represents the magnitude of the stresses; from blue (zero value) to red (high value, 1 MPa). Interestingly, the region where particles experience the highest stresses is not at the constriction point/gap between the push arm and the vessel wall, but the region before that where jamming/pinching occurs, leading to pile up. Another region of high stress concentration is at the scraper front, where the particles get ploughed off the vessel wall, though at a lower intensity. Particle shape has a prominent influence on the prevailing stresses as can clearly be seen in the videos. The tomahawk shape of the lactose monohydrate crystals promotes particle interlocking and limit their ability to rearrange themselves upon being sheared. This increases the bulk friction of the assembly of particles significantly as demonstrated by the large red patch right next to the push arm. Paracetamol crystals, due to their more rounded shape, have a stress distribution profile which is closer to those of spheres, showing lower stresses are experienced by the particles, despite the fact that they are all being operated under the same conditions.

What did we learn from this exercise?

Particle shape does matter. It changes the particle interaction during the mixing process.
Regions of high stresses. The region where particles experience the highest stress is before the particles enter the gap between the push arm and the vessel wall, where jamming occurs.
The amount of particles in the system and the gap size are important. There will be no shearing for a low quantity, and hence no mixing/coating, if the gap size is bigger than the thickness of the particle bed. This can be circumvented by increasing the amount of particles or decreasing the gap size at the constriction point.

Acknowledgement

This work is supported by the Engineering and Physical Sciences Research Council (grant number EP/R001766/1) as a part of ‘Friction: The Tribology Enigma’ (www.friction.org.uk), a collaborative Programme Grant between the universities of Leeds and Sheffield.

We are thankful to ESSS, Florianopolis, Brazil, for providing a special license for the Rocky software for use in this work.

Mechanofusion is a preparatory item of equipment of Hosokawa Micron, whose support for experimental validation (not reported here) is gratefully acknowledged.